强关联多体量子系统研究的复杂性随着粒子数的增长而指数增加，远远超过了当今计算机所能处理的复杂度，这就是1999年诺贝尔化学奖获得者Walter Kohn在他的获奖报告中提到的所谓“指数墙”问题，也是研究强关联量子问题面临的最大挑战之一。为了解决这个问题，强关联量子理论近年来受到广泛关注的一个研究方向就是发展张量重正化群方法。张量重正化群是一种通过波函数或作用量的张量网络态表示，并运用重正化群变换来研究多体量子问题的方法。这种方法满足变分原理和量子纠缠熵的面积定律，并且不存在量子蒙特卡罗方法中遇到的“负符号”（或负概率）问题，是一种普适的多体研究方法，在强关联量子问题的研究方面有广泛的发展和应用前景。
　　但是，要把张量重正化群真正发展成为一个高效和全面研究量子多体问题的方法，还有许多问题需要解决。中国科学院物理研究所/北京凝聚态物理国家实验室（筹）凝聚态理论与计算重点实验室T06组向涛研究员的课题组及其合作者长期从事这方面的研究。2008年，他们提出了一种把量子纠缠作为场量的平均场方法，建立了高效计算张量乘积态波函数的方法 (PRL 101,090603（2008）)，2009年在此基础上，又提出了通过这种波函数精确计算物理量的二次重正化群方法 (PRL 103,160601(2009))。2012年，他们进一步提出了基于高阶奇异值分解的张量重正化群方法，建立了精确研究三维经典统计模型热力学性质的计算方法，把通过重正化群计算三维伊辛模型临界温度的精度提高了五个量级，超过了蒙特卡罗和其它方法对三维问题研究的计算精度(PRB 86, 045139(2012))。与此同时，他们也在努力探索和发展精确研究量子阻挫问题的张量重正化群方法。
　　量子阻挫是凝聚态理论研究的一个基本问题，这个问题之所以值得研究，是因为量子阻挫系统中存在一种新的量子态---量子自旋液体态，它们具有丰富的拓扑量子序，可能是莫特绝缘体真正的基态。如果能从实验上找到这种新的量子态，不仅对量子阻挫本身的研究具有重要意义，而且对于高温超导机理的研究也会有很大的帮助。但是，量子阻挫问题理论研究非常困难：一是在量子阻挫系统中，量子涨落很强，并且存在多种有序态相的竞争，解析研究很困难；二是对于这类系统，量子蒙特卡罗方法存在负符号问题，密度矩阵重正化群及其它计算方法也都存在许多问题，结果的可靠性不能保证。
　　用张量重正化群方法解决量子阻锉问题，这是张量重正化群研究的一个很重要的目标，但很长一段时间一直没有任何进展。最近，向涛研究组与中国人民大学Bruce Normand教授合作发现，造成这个问题的原因，是因为过去所用的张量乘积态波函数只是强调两粒子之间的量子纠缠，而在一个量子阻挫系统中，例如图(1a)所示的Kagome格子系统中，在考虑多粒子之间的相互作用之后，这些两粒子之间的量子纠缠相互抵消，真正起作用的是三体或三体以上的量子纠缠效应。为了正确刻画这种多体量子纠缠，他们提出了一种新的张量网络态波函数，这种波函数能够严格描述每个几何单形（simplex）上的三体或更多体的量子纠缠，被称之为投影纠缠单形态(PESS)。几何单形是构成二维或高维晶格的基本单元，例如三角形就是图(1a)所示的Kagome格子的一种几何单形，一个几何单形包含至少三个格点。此外，对Kagome格子，这种波函数是定义在几何单形的中心所构成的没有阻挫的六角格子上（图(1b)），消除了由于几何阻挫给计算带来的复杂性。在此基础上，他们对Kagome格点上自旋1/2反铁磁海森堡模型做了初步研究，在每个方向仅保留13个状态的情况下，所得到的基态能量就已经可以和经过外插的大规模变分蒙特卡罗和密度矩阵重正化群的最优结果一致（图2），充分显示了这种张量波函数在研究量子阻挫问题方面所具有的潜力。这项工作为解决量子阻挫问题奠定了很好的基础，是量子阻挫问题研究的一个重要进展。他们下一步就是希望通过增加保留的状态数，对关联函数和拓扑纠缠熵进行系统的计算，澄清Kagome海森堡模型是否存在量子自旋液体这个争论了二十多年的问题。
　　这项研究成果最近发表在Phys. Rev. X4, 011025 (2014)。该工作得到了国家自然科学基金和科技部973计划的支持。
　　文章链接：Z.Y. Xie, J. Chen, J.F. Yu, X. Kong, B. Normand, and T. Xiang, Tensor Renormalization of Quantum Many-Body Systems Using Projected Entangled Simplex States, Phys. Rev. X 4, 011025 (2014). http://journals.aps.org/prx/abstract/10.1103/PhysRevX.4.011025

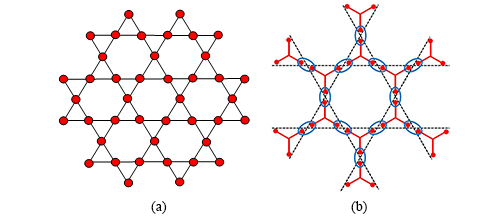图1. (a) Kagome格子。(b) 投影纠缠单形态的图形表示。每个Y型的图案是一个三体最大纠缠态，椭圆蓝线包围的两个圆点表示相邻两个纠缠态向物理态的投影。它们合在一起构成了一个张量网络态。

图2. 通过投影纠缠单形态计算得到的Kagome海森堡模型的基态能量随张量维数的变化，及其与其它方法得到的结果的比较。